Красивые места на Земле: Мастер-класс

Прогрессия - последовательность чисел, получаемых по некоторому правилу.

Арифмети́ческая прогре́ссия (алгебраическая) — числовая последовательность вида

a_1,\ a_1+d,\ a_1+2d,\ \ldots,\ a_1+(n-1)d, \ \ldots

то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа

d

(шага, или разностипрогрессии):

a_n=a_{n-1} + d \quad

Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:

a_n=a_1 + (n-1)d

Геометри́ческая прогре́ссия — последовательность чисел

b_1,\ b_2,\ b_3,\ \ldots

(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число

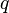q \quad

(знаменатель прогрессии), где

b_1\not=0

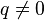q\not=0

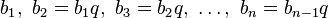
b_1,\ b_2=b_1q,\ b_3=b_2q,\ \ldots,\ b_n=b_{n-1}q

Прогрессии широко встречаются в окружающей нас жизни.Прогрессии в природе.

Все организмы обладают интенсивностью размножения в геометрической прогрессии. Примеры этих организмов:

ИНФУЗОРИИ… Летом инфузории размножаются бесполым способом делением пополам.

Вопрос: сколько будет инфузорий после 15-го размножения?

Ответ: b15 = 2·214 = 32 768 (геометрическая прогрессия)

БАКТЕРИИ…

Бактерия, попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т.д. Найдите число бактерий, образующихся из одной бактерии к концу суток.

Решение. В сутках 1440 минут, каждые двадцать минут появляется новое поколение - за сутки 72 поколения. По формуле суммы n первых членов геометрической прогрессии, у которой b1=1, q=2, n=72, находим, что S72=272-1= 4 722 366 482 869 645 213 696 - = 4 722 366 482 869 645 213 695

Это число читается:

Всего бактерий

4 септиллиона

722 сектиллиона

366 квинтиллионов

482 квадриллионов

869 триллиона

645 миллиарда

709 миллионов

213 тысяча 695

МУХИ……“Потомство пары мух съест мёртвую лошадь также скоро как лев”. Карл Линней.

Девятое поколение одной пары мух наполнило бы куб, сторона которого равна 140 км, или же составило бы нить, которой можно опоясать земной шар 40 млрд. раз. (пример геометрической прогрессии).

ОДУВАНЧИК……. “Потомство одного одуванчика за 10 лет может покрыть пространство в 15 раз больше суши

земного шара”.

Задачи:

Одно растение одуванчика занимает на земле площадь 1 кв. метр и даёт в год около 100 летучих семян.

а) Сколько кв. км площади покроет всё потомство одной особи одуванчика через 10 лет при условии, если он размножается беспрепятственно по геометрической прогрессии?

Ответ: 1012 км2

б) Хватит ли этим растениям на 11-й год места на поверхности суши земного шара?

Ответ: нет, Sсуши = 148 млн км2

В каких процессах ещё встречаются такие закономерности?

Деление ядер урана происходит с помощью нейронов. Нейтрон, ударяя по ядру урана раскалывает его на две части. Получается два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывают их еще на 4 части и т.д. — это геометрическая прогрессия.